Super Matrix Solver P-ICCG の特長 |
|
■電磁場解析、構造解析など様々な解析分野で利用可能な実績のある解法です。
■環境変数の設定のみで多コアCPUを活用した並列計算が可能
■実行形式(DLLなど)で提供-容易に組込可能
|
ICCG法とは |
|
■ICCG法は、CG(共役勾配)法をベースとし、前処理技術(不完全コレスキー分解:Incomplete Cholesky)により、CG法を高速化した反復解法です。前処理の無いCG法に比べ高速で安定な解法です。
■構造解析、電磁場解析、数値流体解析などの広い解析分野で利用されており、利用実績の多い反復解法です。
|
P-ICCGの概略仕様 |
| 項目 |
内容 |
備考 |
| 対象とする解析分野 |
構造解析・電磁場解析など |
|
| 対象とする係数行列 |
有限要素法、有限体積法、差分法などの離散化手順により作成される疎行列 |
|
| 対角に0要素のある問題 |
計算可能 |
全ての0要素問題が解ける訳ではありません |
| 要素のデータ型 |
実数(倍精度)及び複素数 |
|
| 問題の対称性 |
対称問題に限定。非対称問題は計算できません |
|
| 並列方式 |
共有メモリ型(SMP)に対応 |
|
| 計算可能CPU数 |
技術上の制限なし。但し,1~8CPU程度での利用を推奨 |
計算CPU数に応じたライセンス契約が必要です。 |
| 入力データ |
係数行列、右辺定ベクトル、収束判定条件、最大反復回数、その他 |
計算に使用するCPU数の指定可能 |
| 出力データ |
解ベクトル、達成相対残差、実反復回数、その他 |
|
| エラーメッセージ |
戻り値としてワーニング、エラーメッセージを返す。
(計算情報、システム情報など) |
|
| 提供方式 |
DLL形式(WINDOWS)、
スタティックライブラリー形式(LINUX) |
ソースコードは開示しません |
| 付属資料 |
説明書(データフォーマット/パラメータ/組込手順などの説明資料)、サンプルデータ,P-ICCG組込用サンプルプログラム(C,FORTRAN) |
|
|
P-ICCGの性能例 |
実計算時間(単位:秒) |
| 問題の種類 |
未知数の数 |
収束時間 [秒] (収束判定条件:相対残差<1.0e-10) |
| 1-CPU |
2-CPU |
4-CPU |
8-CPU |
| 電磁場解析 |
約22万元 |
87.0 |
43.6 |
26.7 |
13.4 |
| 流体解析 |
約50万元 |
78.3 |
54.2 |
32.7 |
19.3 |
| 構造解析 |
約25万元 |
1227.5 |
744.7 |
390.4 |
224.1 |
| 流体解析 |
約100万元 |
178.5 |
141.7 |
82.7 |
48.5 |
|
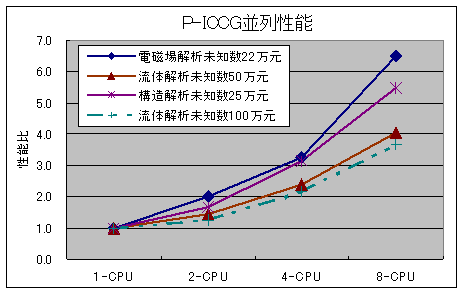
1CPUの計算時間を1とした場合の計算性能比 |
| 問題の種類 |
未知数の数 |
収束時間比(収束判定条件:相対残差<1.0e-10) |
| 1-CPU |
2-CPU |
4-CPU |
8-CPU |
| 電磁場解析 |
約22万元 |
1.0 |
2.0 |
3.3 |
6.5 |
| 流体解析 |
約50万元 |
1.0 |
1.4 |
2.4 |
4.1 |
| 構造解析 |
約25万元 |
1.0 |
1.6 |
3.1 |
5.5 |
| 流体解析 |
約100万元 |
1.0 |
1.3 |
2.2 |
3.7 |
|
|
|
適用事例 |
カタログ/資料ダウンロードページに下記の資料がございますので、ダウンロードしてご利用ください。
■電磁界解析ソフトJMAGへのP-ICCG組込について
(H15年VINAS秋セミナーにおける日本総合研究所様ご発表資料)(PDFファイル/320KB)
|
詳細資料 |
カタログ/資料ダウンロードページに下記の資料がございますので、ダウンロードしてご利用ください。
■P-ICCG製品情報(PDFファイル/437KB)
|
